এইচএসসি পদার্থবিজ্ঞান ১ম পত্র এর ২য় অধ্যায়ের (ভেক্টর) একটি গুরুত্বপূর্ণ বিষয় নদী-নৌকা-নদীর স্রোত সম্পর্কিত গাণিতিক সমস্যাগুলো। এই অধ্যায় থেকে এরকম প্রশ্ন এইচএসসিতে সৃজনশীল, বহুনির্বাচনি উভয় জায়গাতেই যেমন করা হয়ে থাকে, তেমনি করা হয়ে থাকে বিশ্ববিদ্যালয়ের ভর্তি পরীক্ষাতেও। আজ আমরা এরকম সকল প্রশ্নের সমাধান যাতে করে সহজেই সমাধান করে ফেলা যায় সেই পদ্ধতিগুলো নিয়ে আলোচনা করব। একই সাথে বিগত বছরগুলোতে বিভিন্ন পরিক্ষায় আসা কিছু প্রশ্নের সমাধানও করব।
প্রথমেই প্রশ্নে দেয়া থাকা কোন রাশিকে কী ধরে নিয়ে সমাধানে এগোবো তা নিয়ে আলোচনা করা যাক।
সূচীপত্র (toc)
দেওয়া আছে যা যা
প্রশ্নে বিভিন্ন সময় বিভিন্ন রাশি দেয়া থাকে। আমরা এসকল রাশির সবগুলোকেই এখানে উল্লেখ করব।
সবসময় এভাবে ধরে নিয়েই সমাধান করা যাবে। তোমরা চাইলে অন্যভাবে করতে পারো, তবে আমি এখানে এগুলো ধরে নিয়েই করব।
- নদীর স্রোতের বেগ = u
- নৌকার বেগ = v
- নৌকার বেগ ও স্রোতের বেগের মধ্যবর্তী কোণ = `\alpha`
- নদীর প্রস্থ বরাবর নৌকার বেগের উপাংশ = vsin`\alpha`
- নদীর দৈর্ঘ্য বরাবর নৌকার বেগের উপাংশ = vcos`\alpha`
- নদীর দৈর্ঘ্য বরাবর স্রোতের বেগের উপাংশ = u
- নদীর প্রস্থ বরাবর স্রোতের বেগের উপাংশ = 0
- নদীর দৈর্ঘ্য বরাবর মোট বেগ পেলাম আমরা u + vcos`\alpha`
- নদী পারাপারের জন্য প্রয়োজনীয় সময় = t
- নদীর প্রস্থ = d
প্রথমে আমরা সময় নির্ণয় করার প্রক্রিয়া জানব।
Task 1: নদী পারাপারের সময় নির্ণয়
নদী পারাপারের জন্য প্রয়োজনীয় সময় কয়েকটি আলাদা আলাদা শর্তে নির্ণয় করতে পারে। এর মধ্যে চারটি হচ্ছে:
- সাধারণ স্রোতে
- ঠিক বিপরীত প্রান্ত থেকে x দূরত্বে
- সর্বনিম্ন দূরত্বে
- সর্বনিম্ন সময়ে
আমরা এই তিনটি নিয়েই আলোচনা করব।
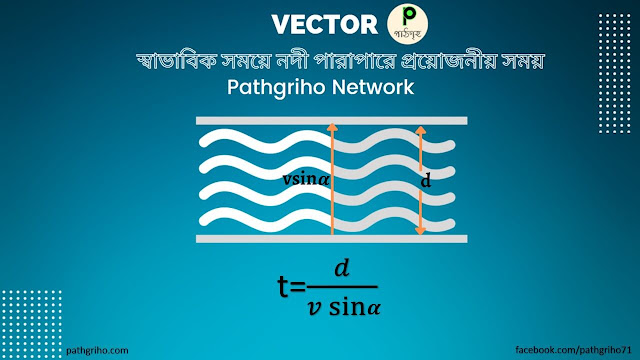
স্বাভাবিক স্রোতে নদী পারাপারের জন্য প্রয়োজনীয় সময় নির্ণয়
স্বাভাবিক অবস্থায় নদী পারাপারের জন্য প্রয়োজনীয় সময় খুবই সহজে নির্ণয় করে ফেলা যায়। এর জন্য আমরা একটি মাত্র সূত্রই ব্যবহার করতে পারি। যদিও এর বাইরে আমরা অন্যান্য সূত্র ব্যবহার করেও (বিশেষ করে পিথাগোরাসের সূত্র) নির্ণয় করতে পারব, তবে আমরা একটি মাত্র সূত্রই অনুসরণ করার চেষ্টা করব।
সমবেগে চলমান কোনো কিছুর কোনো দূরত্ব অতিক্রম করতে প্রয়োজনীয় সময়ের জন্য আমরা দূরত্বকে বেগ দ্বারা ভাগ করি। এখানেও একই কাজ করতে হবে। তবে বেগ দিয়ে ভাগ না করে বেগের প্রস্থ বরাবর নৌকার বেগের উপাংশ দিয়ে ভাগ করতে হবে। অর্থাৎ,
নদী পারাপারের প্রয়োজনীয় সময়, `t=\frac d{v\sin\alpha}`
যেখানে, d = নদীর প্রস্থ, v = নৌকার বেগ এবং `\alpha` = নৌকার বেগ ও স্রোতের বেগের মধ্যবর্তী কোণ।
অর্থাৎ, এক্ষেত্রে, `t=\frac d{v\sin\alpha}`
উদাহারণের মাধ্যমে আমরা বুঝে নেয়ার চেষ্টা করি।
উদাহারণ ১
প্রতি ঘন্টায় 1800 m বেগে 240 m প্রশস্ত একটি নদী নিচের দিকে প্রবাহিত হচ্ছে এবং প্রতি ঘন্টায় 3600 m বেগে সাঁতার কাটতে সক্ষম এমন একজন সাঁতারু নদীর বিপরীত একটি প্রান্তে যেতে ইচ্ছুক বলে সে `120^\circ` কোণ করে সাঁতার দিলো। সেই বিন্দুতে পৌঁছাতে তিনি কত সময় নেবে? [বুয়েট ভর্তি পরীক্ষা ২০০৩-'০৪]
সমাধান: আমরা জানি, `t=\frac d{v\sin\alpha}`
বা, `t=\frac{240}{3600\times\sin(120)}`
বা, `t=0.07698` ঘন্টা
সর্বনিম্ন দূরত্ব বা ন্যূনতম দূরত্ব পার করতে কত সময় লাগবে?
সর্বনিম্ন দূরত্ব বা ন্যূনতম পার করা বলতে বুঝায় সরাসরি নদীর প্রস্থ বরাবর নদী পার হওয়া, সর্বনিম্ন দূরত্বে নদী পার হওয়া বলতে বুঝায় ঠিক অপর প্রান্তে পৌঁছানো। এখন ঠিক অপর প্রান্তে পৌঁছাতে চাইলে আগে জানতে হবে ঠিক কত কোণে নৌকা চালনা করতে হবে। আমরা ধরে নিলাম `\alpha` কোণ করে চালাতে হবে, ফলে তার লব্ধি নৌকার স্রোতের দিকের সাথে `90^\circ` কোণ করে থাকে। (ঠিক অপর প্রান্তে পৌঁছাতে কত কোণ করে চালাতে হবে তা নিচে আলাদাভাবে উল্লেখ করা হয়েছে।)
এবার বাকি সব কিছুই স্বাভাবিক স্রোতে নৌকা দিয়ে নদী পার হওয়ার সময় নির্ণয়ের পদ্ধতির মতোই।
`t=\frac d{v\sin\alpha}`
উদাহারণ ২
একটি নদীতে স্রোতের বেগ ঘন্টায় 6 কিলোমিটার এবং নৌকার বেগ ঘন্টায় 12 কিলোমিটার। নদীর প্রস্থ এখানে 10 কিলোমিটার। সর্বনিম্ন দূরত্বে নৌকাটিকে পার করতে হলে `120^\circ` কোণে চালাতে হবে। সর্বনিম্ন দূরত্ব কত? কত সময় প্রয়োজন হবে?
সমাধান: সর্বনিম্ন দূরত্ব = নদীর প্রস্থ = 10 km
প্রয়োজনীয় সময় = `t=\frac d{v\sin\alpha}`
বা, `t=\frac{10}{12\times\sin(120)}`
বা, `t=0.96225` ঘন্টা
সর্বনিম্ন সময়ে বা ন্যূনতম সময়ে নদী পার হতে কত সময় লাগবে?
সর্বনিম্ন সময়ে নদী পার করতে হলে sin`\alpha` এর মান সর্বোচ্চ হতে হবে। আমরা জানি, sin`\alpha` এর সর্বোচ্চ মান 1 যা আমরা পাবো যদি `\alpha=90^\circ`হলে। এক্ষেত্রে তাহলে সূত্রটি দাঁড়াবে,
`t=\frac d{v\sin\alpha}` বা, `t=\frac d{v}` [যেহেতু `sin\alpha` = 1]
Task 2: কোন দিকে চললে ঠিক অপর পারে পৌঁছাতে পারবে?
এটি এরও একটি গুরুত্বপূর্ণ প্রশ্ন। অনেক সময় প্রশ্নে বলা থাকে,
- মাঝি/সাঁতারু নদীর ঠিক অপর পারে পৌঁছাতে চায় বলে নদীর প্রস্থ বরাবর চলতে শুরু করলো। সে কি ঠিক অপর বিন্দুতে পৌঁছাতে পারবে?
- যাত্রাবিন্দু থেকে ঠিক বিপরীত প্রান্ততে পৌঁছাতে চাইলে কোন দিক বরাবর রওনা দিতে হবে?
প্রথম প্রশ্নের উত্তর নিঃসন্দেহে হবে "না, পৌঁছাতে পারবে না। কারণ যেহেতু নদীতে স্রোত আছে তাই স্রোত নৌকাকে ঠেলে তার লক্ষ্য থেকে সরিয়ে দেবে।" তাই বিপরীত প্রান্তে পৌঁছাতে হলে তাকে আরও বেশি বেঁকে গিয়ে নৌকা চালাতে হবে বা সাঁতার কাটতে হবে যাতে করে স্রোত তাকে ঠেলে নিয়ে ঠিক বিপরীত প্রান্তে নিয়ে পৌঁছে দেয়। এমন সমস্যার সমাধান আমরা করব দুটি নিয়মে। একটি মূল নিয়মে এবং সৃজনশীল প্রশ্নের উত্তর এভাবেই করতে হবে। অন্যটি শর্টকাট যা দিয়ে এমসিকিউ করতে পারবে এবং বিশ্ববিদ্যালয়ের ভর্তি পরীক্ষায় উত্তর করতে পারবে। সৃজনশীল প্রশ্নের উত্তর করতে গিয়ে যদি সময় কম থাকে তবে সেখানেও এভাবে করে দিলে কিছু মার্কস পাওয়া যাওয়ার কথা। তাহলে আমরা দেখে নিই দুটি নিয়মই এবং তা উদাহারণের মাধ্যমেই।
উদাহারণ ৩
সোজা অপর পাড়ে যাওয়ার জন্য বাবুল ফেরিতে করে 15 km/h বেগে নদী পার হওয়ার সময় দেখল ফেরিটি সোজাসুজি রওনা না দিয়ে স্রোতের প্রতিকূলে তীর্যকভাবে যাচ্ছে যেখানে স্রোতের বেগ 10 km/h। ফেরিটির কোন দিক বরাবর যাচ্ছে?
মূল নিয়ম
আমরা আগেই বলেছি স্রোত যুক্ত নদীতে ঠিক অপর পারে পৌঁছাতে গেলে তীর্যকভাবেই (স্রোতের বিপরীত দিকে) রওনা দিতে হয়, এই কারণেই ফেরিটি দিক বদলেছে। এখন ফেরিটি কোন দিক বরাবর যাচ্ছে তা আমাদেরকে নির্ণয় করতে হবে। নির্ণয়ের জন্য আমরা নিচের নিয়ম অনুসরণ করতে পারি।
মনে করি, স্রোতের বেগ = u এবং নৌকার বেগ = v
তাহলে একদম শুরুতেই আমরা যেভাবে বলেছিলাম,
- নদীর প্রস্থ বরাবর নৌকার বেগের উপাংশ = vsin`\alpha`
- নদীর দৈর্ঘ্য বরাবর মোট বেগ পেলাম আমরা u + vcos`\alpha`
তাহলে এখন আমরা `\theta` কোণের tan অনুপাত নিলে পাই,
`\tan\theta=\frac{v\sin\alpha}{u+v\cos\alpha}`
বা, `\tan90=\frac{v\sin\alpha}{u+v\cos\alpha}`
বা, `\frac{1}{0}=\frac{v\sin\alpha}{u+v\cos\alpha}`
বা, `u+v\cos\alpha=0`
বা, `\cos\alpha=\frac{-u}v=-\frac{10}{15}`
বা, `\alpha=\cos^{-1}(\frac{-10}{15})`
বা, `\alpha=131.8^\circ`
এভাবে করতে হবে যদি সৃজনশীল প্রশ্নে আসে। কিন্তু বিশ্ববিদ্যালয় ভর্তি পরীক্ষার জন্য এবং অন্যান্য পরীক্ষার এমসিকিউয়ের উত্তর করার জন্য নিচের শর্টকাটটি ফলো করলেই হবে। এই শর্টকাটটি মূলত উপরের প্রক্রিয়ার শেষ লাইনটিই।
শর্টকাট
`\alpha=\cos^{-1}(\frac{-u}v)` এই সূত্র দিয়ে করে ফেললেই হয়ে যাবে। এখানে আমরা u এবং v ধরেছি যথাক্রমে স্রোতের বেগ এবং নৌকার বেগকে। অনেক বইতে উলটোভাবেও ধরা থাকে। কনফিউজড হওয়ার কিছু নেই। সোজা সাপ্টা, `\alpha=\cos^{-1}`(-স্রোতের বেগ/নৌকার বেগ)
এক্ষেত্রে বিশেষ একটি সুবিধা হলো, বেশিরভাগ ক্ষেত্রেই নৌকার বেগ থাকে স্রোতের বেগের দ্বিগুন। যেখানেই এমন পাবে সেখানেই চোখ বন্ধ করে উত্তর লিখে দিবে `120^\circ`। কেন এমনটা হলো? উপরের সূত্র দিয়ে নিজেরাই করে দেখ।
Task 3: লব্ধি ও দূরত্ব নির্ণয়
সর্বনিম্ন সময়ে পার হলে লব্ধি ও দূরত্ব
সর্বনিম্ন সময়ে নদী পার হলে লব্ধি হবে `w=\sqrt{(v^2+u^2)}`
এক্ষেত্রে দূরত্ব হবে, `d=vt`
সর্বনিম্ন দূরত্ব পার করতে চাইলে লব্ধি ও দূরত্ব
এক্ষেত্রে লব্ধি হবে `w=\sqrt{(v^2-u^2)}`
এবং দূরত্ব হবে `d=wt=\sqrt{(v^2-u^2)}\timest`
সর্বনিম্ন দূরত্ব কত?
নদীর প্রস্থই সর্বনিম্ন দূরত্ব।
এই টপিকের মূল কয়েকটি টাইপের সমস্যা এগুলোই। এর বাইরে আরও কিছু প্রশ্ন হয়ে থাকে যেগুলোর মধ্য থেকে গুরুত্বপূর্ণ আর এক ধরণের গাণিতিক সমস্যার সমাধান আমরা দেখব।
Task 4: স্রোতের বেগ নির্ণয়
উপরে যতগুলো সমস্যার সমাধান করেছি তাতে স্রোতের বেগ রয়েছে। সেখান থেকেই স্রোতের বেগ নির্ণয় করতে বলতে পারে পরীক্ষায় যদিও এমন প্রশ্ন খুব একটা হয়নি। তবে স্রোতের বেগ সম্পর্কিত যে প্রশ্ন কিছুটা কমন তার একটি উদাহারণ আমরা নিচে দেখে নিই।
উদাহারণ ৪
স্রোত না থাকলে একজন লোক 4 মিনিটে সাঁতার কেটে আড়াআড়িভাবে 100 মিটার প্রশস্ত একটি নদী অতিক্রম করতে পারবে এবং স্রোত থাকলে পারে 5 মিনিটে। স্রোতের বেগ নির্ণয় কর।
সমাধান: স্রোতের বেগ u এবং লোকটির বেগ ও স্রোত থাকাকালীন লব্ধি w হলে,
v = 100/4 = 25 m/min
w = 100/5 = 20 m/min
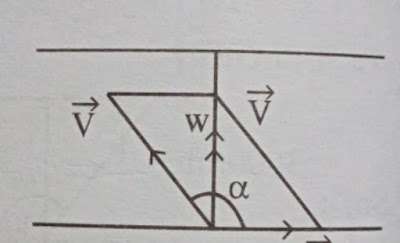
ভেক্টরকে তার মান ও দিক অপরিবর্তিত রেখে যেহেতু সরিয়ে নেয়া যায়, সেহেতু আমরা নিচের চিত্রের মতো করতে পারি এবং সেখান থেকে পিথারোগারের সূত্র ব্যবহার করে নির্ণয় করে ফেলতে পারি স্রোতের বেগ বা u।
এখন, পীথাগোরাসের সূত্র থেকে আমরা পাই,
`v^2=w^2+u^2`
বা, `u^2=v^2-w^2`
বা, `u=15` m/min
উল্লেখ্য, আমরা স্রোতের বেগ এবং নৌকার বেগকে u এবং v ধরে নিয়ে সমাধান করেছি সবকিছু। এখানে আপনি অন্য বইতে উল্টোভাবে পেতে পারেন। এই বিষয়টি নজরে রাখতে বলা হচ্ছে।
পাশাপাশি আমাদের এই লেখায় কোনো ভুল পেলে তা আমাদের অবহিত করুন আমাদের Contact Us পেজ থেকে। কোনো ধরণের সমস্যা থাকলে যোগাযোগ করুন আমাদের ফেসবুক পেজে। ধন্যবাদ।
আরও পড়ুন