গণিতের জগতে যতগুলো বহুল ব্যবহৃত উপপাদ্য রয়েছে তার মধ্যে পিথাগোরাসের উপপাদ্য অন্যতম একটি। সমকোণী ত্রিভুজ নিয়ে কাজ করতে গেলেই পিথাগোরাসের উপপাদ্য যেন লাগবেই। আজ আমরা শিখব এই উপপাদ্যটি।
পিথাগোরাসের উপপাদ্য
কোনো সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুই বাহুর উপর অঙ্কিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের সমষ্টির সমান।
মূল উপপাদ্য শুরুর আগে আমরা একটু এই বিবৃতিটি বুঝার চেষ্টা করি। প্রথমেই বুঝতে হবে অতিভুজ কী? এবং সমকোণী ত্রিভুজ কী? সমকোণী ত্রিভুজের সংজ্ঞা জানতে পড়ুন: সমকোণী ত্রিভুজ।
অতিভুজ কাকে বলে?
সমকোণী ত্রিভুজের সমকোণের বিপরীত বাহুকে অতিভুজ বা Hypotenuse বলে।
তাহলে উপপাদ্য থেকে আমরা কী বুঝলাম? বুঝতে পারলাম কোনো সমকোণী ত্রিভুজের যে কোনটি সমকোণ তার বিপরীত বাহু বা অতিভুজের স্কোয়ারের মান হবে অন্য দুই বাহু (ভূমি এবং লম্বের) এর আলাদা আলাদা স্কোয়ারের যোগফলের সমান। এবার আমরা উপপাদ্যটি প্রমাণের চেষ্টা করি।
বিশেষ নির্বচন
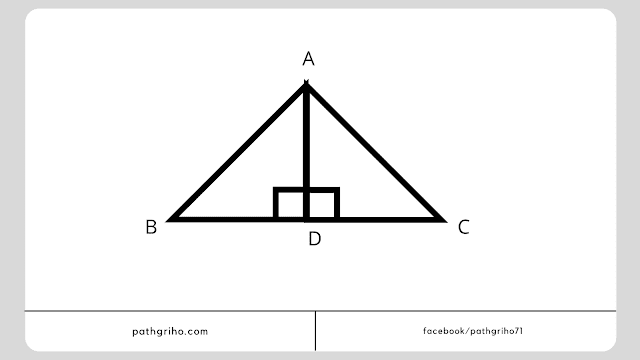
ধরি, `\triangle ABC` একটি সমকোণী ত্রিভুজ যার `\angle A` = এক সমকোণ। অর্থাৎ BC বাহু এর অতিভুজ। প্রমাণ করতে হবে যে, `BC^2 = AC^2+AB^2`।
অঙ্কন
`\triangle ABC` এর A বিন্দু থেকে অতিভুজ BC এর উপর AD লম্ব অঙ্কণ করি। AD লম্ব BC কে D বিন্দুতে ছেদ করে। এই অবস্থায় `\angle D` আলাদা দুটি ত্রিভুজেরই সমকোণ এবং এক্ষেত্রে অতিভুজদ্বয় হলো AB এবং AC।
প্রমাণ
সমকোণী ত্রিভুজটির অতিভুজ BC এর উপর লম্ব হচ্ছে AD। অতএব, `\triangle ABC` এবং `\triangle ABD` সদৃশ।
সুতরাং আমরা লিখতে পারি, `\frac{AB}{BC}=\frac{BD}{AB}`
বা, `AB^2=BD\times BC` যা (i) নং সমীকরণ
আবার, অনুরূপভাবে `\triangle ABC` এবং `\triangle ACD` ও সদৃশ এবং ফলে আমরা অনরূপভাবেই লিখতে পারি, `AC^2=BC\times DC` যা (ii) নং সমীকরণ।
এখন (i) ও (ii) যোগ করে পাই,
`AB^2+AC^2=BD\times BC+DC\times BC`
বা, `AB^2+AC^2=BC(DC+BD)`
বা, `AB^2+AC^2=BC 'times BC` [যেহেতু `BD+DC=BC`]
বা, `AB^2+AC^2=BC^2`
পিথাগোরাসের উপপাদ্যটি প্রমাণিত।
পিথাগোরাসের উপপাদ্য নিয়ে আরও কিছু তথ্য
পিথাগোরাসের উপপাদ্য ইউক্লিডীয় জ্যামিতির অন্তর্ভূক্ত। এই উপপাদ্যটি পিথাগোরাস নামক গ্রিক গণিতবিদের নাম অনুসারারে নামাঙ্কিত করা হয়েছে। এর ধারণা তারও অনেক আগে থেকেই চীনে গৌউযু থিউরি" নামে প্রচলিত ছিলো। পিথাগোরাসের উপপাদ্যের বাস্তব প্রয়োগ করা হয় অনেক ক্ষেত্রেই যার মধ্যে অন্যতম কয়েকটি ক্ষেত্র হলো স্থাপত্য, দিকনির্দেশনা, দূরত্বের পরিমাপের ক্ষেত্রে ইত্যাদি। পিথাগোরাসের উপপাদ্যকে 'বৌদ্ধায়নের উপপাদ্য'ও বলা হয়ে থাকে। কারণ খ্রিস্টপূর্ব প্রায় ৮০০ এর দিকে বৌদ্ধায়ন নামক এক ভারতীয় গণিতজ্ঞ অনেকটা এরূপ একটি উপপাদ্য বর্ণনা করেছিলেন।
মজার বিষয় হচ্ছে, পিথাগোরাসের উপপাদ্যের একটি বিপরীত উপপাদ্যও রয়েছে যা আমরা আলাদাভাবে জানব। আজ এ পর্যন্তই।