রাশি ২ প্রকার। যথা:
- স্কেলার রাশি
- ভেক্টর রাশি
ভেক্টর রাশি সম্পূর্ণরূপে প্রকাশের জন্য মান ও দিক উভয়ের প্রয়োজন। ভেক্টর লব্ধির মান ও দিক নির্ণয়ের পদ্ধতি জানবো আমরা এই লেখা থেকে।
দুটি ভেক্টরের মধ্যবর্তী কোণ
লব্ধি ভেক্টরের মান নির্ণয়ের আগে আমাদের জানতে হবে দুটি ভেক্টরের মান এবং এদের অন্তরভূক্ত কোন কত? দুটি ভেক্টরের মান সরাসরি যদি দেয়া থাকে তবে ভেক্টরদ্বয়ের মধ্যবর্তী অন্তর্ভূক্ত কোণ নির্ণয় করতে হবে। ভেক্টরদ্বয়ের অন্তর্ভূক্ত কোণ নির্ণয়ের জন্য ভেক্টরদ্বয়ের শীর্ষবিন্দু দুটি একই স্থানে মিলিত হতে হবে নয়তো আদিবিন্দু দুটি একই স্থানে মিলিত হতে হবে। এইভাবে যে কোণ উৎপন্ন হবে তাই ভেক্টরদ্বয়ের মধ্যবর্তী অন্তর্ভূক্ত কোন।
একটি ভেক্টরের আদি বিন্দু এবং অপর ভেক্টরের শীর্ষবিন্দু মিলিত হলে সেখান থেকে ভেক্টরকে সমান্তরালে স্থানান্তরিত করে দুটি আদি বিন্দু বা দুটি শীর্ষ বিন্দু এক জায়গায় মিলিত করে কোন নির্ণয়ে করতে হবে। নিচের ছবিতে দেখি।
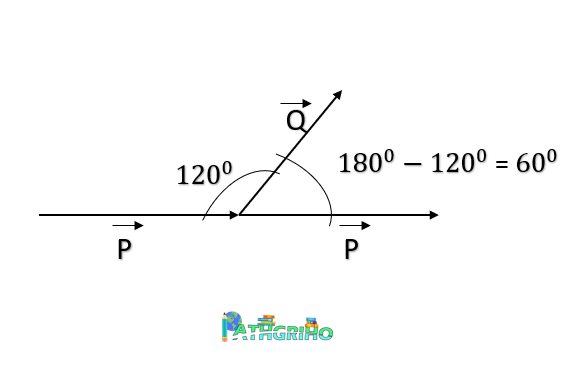
এই ছবিতে যে ১২০ ডিগ্রি কোণ দেখা যাচ্ছে তা আসলে একটি ভেক্টরের শীর্ষের সাথে অন্য ভেক্টরের আদি বিন্দু মিলিত হয়ে গঠিত। এক্ষেত্রে এই ১২০ ডিগ্রি কোণ আসলে এই দুই ভেক্টরের মধ্যবর্তী কোণ না। তাহলে এই দুই ভেক্টরের মধ্যবর্তী কোণ কিভাবে নির্ণয় করব?
নিচের ছবিটি দেখা যাক।
এই ছবিতে দেখা যাচ্ছে P ভেক্টরটিকে সমান্তরালে স্থানান্তরিত করা হয়ে মান ও দিক একই রেখে। এমন ভাবে স্থানান্তারিত করা হয়েছে যাতে P এবং Q ভেক্টরের আদি বিন্দু একই স্থানে আছে। তাই এবার যে কোণ সৃষ্টি হবে তাই হবে ভেক্টরদ্বয়ের মধ্যবর্তী কোণ।
এখানে P ভেক্টরকে সরানো হলে আগের P ভেক্টরের হিসেবে একটি সরলরেখা উৎপন্ন হয়। আমরা জানি সরলরেখা ১৮০ ডিগ্রি। তাই ১৮০ থেকে আগের ১২০ বাদ দিলে যে ৬০ ডিগ্রি পাওয়া যায়, তাই এক্ষেত্রে মধ্যবর্তী কোণ।
লব্ধি ভেক্টরের মান নির্ণয়
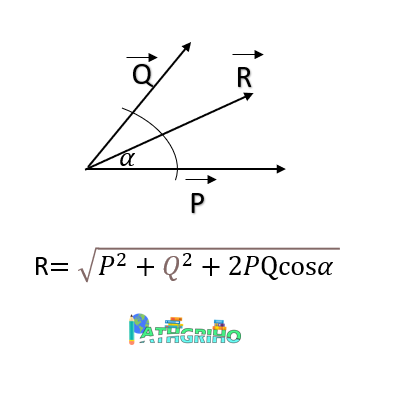
দুটি ভেক্টরের মান P এবং Q এবং ভেক্টর দুটির মধ্যবর্তী কোণ `alpha` হলে লব্ধি ভেক্টর R এর মান হবে,
`R=\sqrt{P^2+Q^2+2PQ\cos\alpha}`
এখানে R ভেক্টর = P ভেক্টর + Q ভেক্টর। বিয়োগের ক্ষেত্রে ছবিটা পাল্টাবে, তবে মান নির্ণয়ের সময় এই একই সূত্র ব্যবহার করেই সঠিক মান পাওয়া যাবে। কারণ দিক বদলালেও, মান বদলাবে না।
লব্ধি ভেক্টরের দিক নির্ণয়
লব্ধি ভেক্টরের দিক নির্ণয় করার জন্য, যে ভেক্টরের সাপেক্ষে নির্ণয় করতে চান, সেই ভেক্টরটিকে নিচে একা রাখতে হবে। অন্য ভেক্টরটিকে উপরে এবং নিচে sin, cos দ্বারা নিচের সূত্রের মতো করতে হবে। যদি আমরা P ভেক্টরের সাথে কত ডিগ্রি কোণ উৎপন্ন করবে তা নির্ণয় করতে চাই, তবে আমাদের সূত্রটি হবে,
`\tan\theta=\frac{Q\sin\alpha}{P+Q\cos\alpha}`
যদি Q ভেক্টরের সাথে কত ডিগ্রি কোণ নির্নয় করতে চাই, তবে সম্পূর্ণ `alpha` থেকে `theta` বিয়োগ করলেই তা পাওয়া যাবে। আবার সূত্রের মাধ্যমেও নির্ণয় করা যাবে। সেক্ষেত্রে সূত্রটি হবে,
`\tan\theta=\frac{P\sin\alpha}{Q+P\cos\alpha}`