এসএসসি সিলেবাসের বিভিন্ন অধ্যায়ের উপর ১০ টি প্রশ্ন ও সমাধান দেয়া হলো।
প্রশ্ন:
১. (1÷9) এর আবৃত দশমিক রূপ কোনটি?
২. X ও Y অক্ষের ছেদবিন্দুকে সর্বপ্রথম কে মূলবিন্দু হিসেবে আখ্যায়িত করেন?
3. একটি কার্ড রিডার 40 টাকায় বিক্রি করলে 10% লাভ হয়। কার্ডরিডারটির ক্রয়মূল্য কত?
৪. দ্বিঘাত সমীকরণের আদর্শ রূপ কোনটি?
5.“Elements” বইটি কোন বিজ্ঞানির দ্বারা কত সালে রচিত?
৬. 15° কোনের পূরক কোন কত?
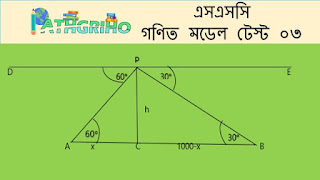
৭. দুইটি কিলোমিটার পোস্ট A এবং B এর মধ্যবর্তী কোনো স্থানের উপর P বিন্দুতে একটি উড়োজাহাজ হতে ওই কিলোমিটার পোস্ট দুটির অবনতি কোন যথাক্রমে 60° এবং 30° হলে উড়োজাহাজটি মাটি থেকে কত উঁচুতে অবস্থিত?
৮. কোনো সমান্তর ধারার m তম পদ m2 (m square), n তম পদ n2 (n square) হলে, ধারাটির (m+n) তম পদ কত?
৯. 6÷2(1+2) =?
১০. সমাধান কর: 1/x + 1/(x+1) = 2/(x-1)
সমাধান:
১. (1÷9) এর আবৃত দশমিক রূপ কোনটি?
উত্তর: 1/9= 0.11111= 0.1 ̇
২. X ও Y অক্ষের ছেদবিন্দুকে সর্বপ্রথম কে মূলবিন্দু হিসেবে আখ্যায়িত করেন?
উত্তর: রেনে দেকার্তে
৩. একটি কার্ড রিডার 40 টাকায় বিক্রি করলে 10% লাভ হয়। কার্ডরিডারটির ক্রয়মূল্য কত?
সমাধান: ধরি, ক্রয়মূল্য x টাকা।
তাহলে,৭% লাভে বিক্রয়মূল্য (x+10x/100) টাকা ।
= x(1+1/10) টাকা
শর্তানুযায়ী, x(1+1/10) = 40
বা, x(11/10) = 40
বা, 11x/10= 40
বা, 11x = 40 × 10 = 400
সুতরাং, x = 400/11 = 36. 363 টাকা।
৪. দ্বিঘাত সমীকরণের আদর্শ রূপ কোনটি?
সমাধান: ax2+bx+c=0
৫. “Elements” বইটি কোন বিজ্ঞানির দ্বারা কত সালে রচিত?
উত্তর: খ্রিষ্টপূর্ব ৩০০ অব্দে।
৬. 15° কোনের পূরক কোন কত?
উত্তর: 75°
৭. দুইটি কিলোমিটার পোস্ট A এবং B এর মধ্যবর্তী কোনো স্থানের উপর P বিন্দুতে একটি উড়োজাহাজ হতে ওই কিলোমিটার পোস্ট দুটির অবনতি কোন যথাক্রমে 60° এবং 30° হলে উড়োজাহাজটি মাটি থেকে কত উঁচুতে অবস্থিত?
সমাধান:
ত্রিভুজ PAC তে tan PAC = PC/AC
tan60 = h/x
√3 = h/x
h = √3x ----(i)
আবার ত্রিভুজ PBC তে, tanPBC = PC/BC
tan30= h/(1000-x)
1/√3 = h/(1000-x)
1000-x = √3h
After Calculating, x = 250 ----- (ii)
সুতরাং, h = √3x = √3 X 250 = 433.013 মিটার (প্রায়)
৮. কোনো সমান্তর ধারার m তম পদ m2 (m square), n তম পদ n2 (n square) হলে, ধারাটির (m+n) তম পদ কত?
সমাধান:
ধরি প্রথম পদ a, সাধারণ অন্তর d
m তম পদ = a+(m-1)d
n তম পদ = a+(n-1)d
শর্তানুসারে,
a+(m-1)d = m2 ---- (i)
a+(n-1)d = n2 ----- (ii)
(i) – (ii) করে পাই,
a+(m-1)d - a+(n-1)d = m2 - n2
…. ….
বা, d = p+q (by solving)
সুতরাং (m+n) তম পদ = a+(m+n-1)d
= a+(m-1)d + nd
= m2+n(m+n)
= m2 + mn + n2
৯. 6÷2(1+2) =?
সমাধান:
6÷2(1+2) = 6÷2×3= 3×3=9
(ক্যালকুলেটরে 1 আসবে যা ভুল)
১০. সমাধান কর: 1/x + 1/(x+1) = 2/(x-1)
সমাধান:
এখানে, 1/x + 1/(x+1) = 1/(x-1) + 1/(x-1)
বা, 1/x - 1/(x-1) = 1/(x-1) - 1/(x+1)
বা, (x-1-x)/x(x-1) = (x+1-x+1)/((x+1)(x-1))
বা, (-1)/x = 2/(x+1)
বা, 3x = -1
… x = -1/3
Tags:
SSC